概述

我又被迫营业了

  • (又是数学内容)

线性代数

  • 算术与代数；线性算术
  • 线性变换
  • 线性变换的应用
    • 计算机图形学
    • 线性方程组

算术与代数；线性算术

算术 (Arithmetic) 和代数 (Algebra)

小学的 “算术”

  • 给一个 “表达式” 和一系列 “等价变换” 规则，求出表达式的值
    • $(3 + 4) \times 5 = 7 \times 5 = 35$
    • $753 + 672 = 1300 + 120 + 5 = 1425$

中学的 “代数”

  • 允许表达式中出现代表某个数值的 “变量”；表达式依然成立
    • $x^2 - 2x - 3 = 0 \Rightarrow x\in \{ -1, 3 \}$

为什么 “代数” 比 “算术” 更难？

  • 算数是 “阅读程序写结果”；代数是 “编程序”
  • 编什么样的程序是不显然的
    • $x^2 - 2x - 3 = 0 \Rightarrow x^2 - 2x + 1 - 4 = 0$

线性系统

“在变量均匀变化时，值也是均匀变化”

  • $z = x + y$ (线性)
  • $z = x \cdot y$ (非线性)

为什么线性系统如此重要？

  • 非线性系统在微观尺度的时候表现是线性的
  • $e^x = 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + \ldots $
    • 这是一个增长很快的函数

线性算术：向量和向量的运算

向量 (vector): 一个 $n$ 维的数组，通常竖着书写

  • 可以理解成平面/空间中的一个点

$$ \vec{x} = \begin{bmatrix} 3 \\ 4 \\ 1 \end{bmatrix}\qquad \vec{y} = \begin{bmatrix} 1.5 \\ -2 \end{bmatrix} $$

向量的 (线性) 算术

  • (加法) 每个维度分别相加
  • (数乘) 每个维度分别乘以同一个常数

$$ \begin{bmatrix} 3 \\ 4 \\ 1 \end{bmatrix} + \begin{bmatrix} -1 \\ 0 \\ 1.5 \end{bmatrix} = \begin{bmatrix} 2 \\ 4 \\ 2.5 \end{bmatrix}\qquad 3 \begin{bmatrix} 3 \\ 4 \\ 1 \end{bmatrix} = \begin{bmatrix} 9 \\ 12 \\ 3 \end{bmatrix} $$

为什么叫 “线性算术”？

加法和乘法的分配律：$x \cdot (a + b) = x \cdot a + x \cdot b$

$$ \begin{bmatrix} x \\ y \\ z \end{bmatrix} = \begin{bmatrix} x \\ 0 \\ 0 \end{bmatrix} + \begin{bmatrix} 0 \\ y \\ 0 \end{bmatrix} + \begin{bmatrix} 0 \\ 0 \\ z \end{bmatrix} = x \begin{bmatrix} 1 \\ 0 \\ 0 \end{bmatrix} + y \begin{bmatrix} 0 \\ 1 \\ 0 \end{bmatrix} + z \begin{bmatrix} 0 \\ 0 \\ 1 \end{bmatrix} $$

空间中的任何一个点都可以写成是三个坐标轴方向的 “相加”

  • 所以 “一个点” 也可以理解成 “源点出发的一个箭头”

线性变换

向量的新运算：线性变换

把三个单位向量 “偷梁换柱”，即可实现任意向量的变换

$$ \begin{bmatrix} 1 \\ 0 \\ 0 \end{bmatrix} { \color{red} \to } \begin{bmatrix} a \\ b \\ c \end{bmatrix} \qquad \begin{bmatrix} 0 \\ 1 \\ 0 \end{bmatrix} { \color{red} \to } \begin{bmatrix} d \\ e \\ f \end{bmatrix} \qquad \begin{bmatrix} 0 \\ 0 \\ 1 \end{bmatrix} { \color{red} \to } \begin{bmatrix} g \\ h \\ i \end{bmatrix} $$

$$ \begin{bmatrix} x \\ y \\ z \end{bmatrix} { \color{red} \to } \begin{bmatrix} ax + dy + gz \\ bx + ey + hz \\ cx + fy + iz \end{bmatrix} $$

大家熟悉的 “矩阵乘向量！”

  • 矩阵的三个列向量分别代表三个坐标轴变换后的新坐标轴

然后……我们会编程啊！

这是一个代表 “坐标变换” 的数学定义：

$$ \begin{bmatrix} a & b & c \\ d & e & f \\ g & h & i \end{bmatrix} \cdot \begin{bmatrix} x \\ y \\ z \end{bmatrix} = \begin{bmatrix} ax + by + cz \\ dx + ey + fz \\ gx + hy + iz \end{bmatrix} $$

我们可以编程把它展现出来！

惊喜时刻

图形 = 点的集合

$$ \begin{bmatrix} a & b & c \\ d & e & f \\ g & h & i \end{bmatrix} \cdot \begin{bmatrix} x \\ y \\ z \end{bmatrix} = \begin{bmatrix} ax + by + cz \\ dx + ey + fz \\ gx + hy + iz \end{bmatrix} $$

不就是图形的变换吗？

  • 能不能在 linear.py 的基础上更进一步
  • 把图形和图形的变换画出来？
    • Linear Transformation: lt.py
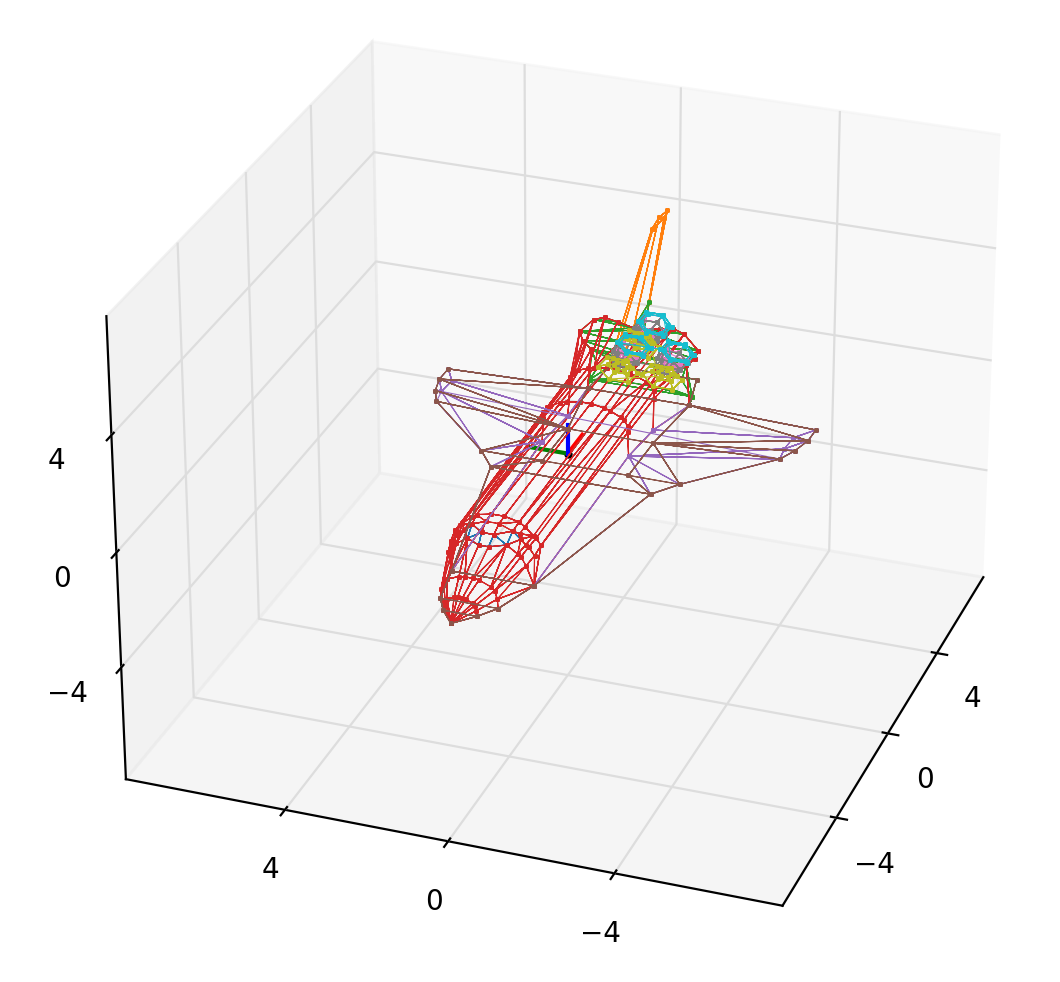
    • 例子：shuttle.obj
      • 这个文件就像是算法竞赛里的输入！

几个特殊的线性变换

$$ \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{bmatrix} \quad \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 0 \\ \end{bmatrix} \quad \begin{bmatrix} 1 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ \end{bmatrix} \quad \begin{bmatrix} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ \end{bmatrix} $$

借助代码，我们生成平滑的 “动画”

  • 在 $t$ 时刻 ($0 \le t \le 1$)，显示 $$(1-t) \begin{bmatrix} x \\ y \\ z \end{bmatrix} + t \left(A \begin{bmatrix} x \\ y \\ z \end{bmatrix}\right) $$
  • 如果只有主对角线上有数值，就对应了坐标轴的拉伸

旋转坐标轴

简单改变一根坐标轴

$$ \begin{bmatrix} 1 \\ 0 \\ 0 \end{bmatrix} { \color{red} \to } \begin{bmatrix} a \\ b \\ c \end{bmatrix} $$

  • 单位立方体被拉伸成了一个平行六面体

一个保持 “单位立方体仍然是单位立方体” 的旋转

$$ \begin{bmatrix} \frac{1}{\sqrt2} & 0 & \frac{1}{\sqrt2} \\ \frac{1}{2} & \frac{1}{\sqrt2} & -\frac{1}{2} \\ -\frac{1}{2} & \frac{1}{\sqrt2} & \frac{1}{2} \\ \end{bmatrix} $$

一些有趣的性质

对于任意线性变换

  • 零永远映射到零
    • $A \cdot 0 = 0$
    • 推论：线性变换无法实现 “平移”
  • 如果没有 “压扁”，就一定存在一个 “复原” 的线性变换
    • 称为 “逆变换”
    • $A^{-1} (A x) = x$
  • 线性变换不可交换
    • 先旋转再拉伸 $\ne$ 先拉伸再旋转
  • 矩阵乘法 = 线性变换的复合
    • 三个向量分别乘矩阵

线性变换与计算机图形学

刚才绘制的图形，是否让你想到 3D 世界？

(The Utah Teapot)

点、线、面：3D 世界的骨架

和刚才的模型 (shuttle) 十分类似

  • 这就是你在游戏里看到的三维场景！
    • 每一帧都计算出点、线、面到视平面的投影
  • 所有的变换都是线性变换！

一些有趣的 Tricks

线性变换不是不能平移的吗？

  • 零永远映射到零
    • $A \cdot 0 = 0$
    • 推论：线性变换无法实现 “移”
  • 在三位空间里不行，但四维空间就可以了
    • grid2D 的例子
    • 投影矩阵的推导就更复杂了
    • 著名的 Games 101 课程 (现代计算机图形学入门)

“为什么玩家更爱使用女角色？”

  • 目前的计算力还不支持游戏实时有限元级的仿真
    • 于是我们看到了各种穿模、空气墙……

线性变换与线性方程组

线性变换意义下的方程组

“鸡兔同笼”

  • 未知数 $x$, $y$ 可以看成未知的向量
  • 在给定的线性变换 $A$ 下，得到 $x' = 10, y' = 32$

$$ \left\{ \begin{matrix} x & + & y & = & 10 \\ 2x & + & 4y & = & 32 \\ \end{matrix} \right. $$

$$ \begin{bmatrix} 1 \\ 0 \\ \end{bmatrix} { \color{red} \to } \begin{bmatrix} 1 \\ 2 \\ \end{bmatrix} \qquad \begin{bmatrix} 0 \\ 1 \\ \end{bmatrix} { \color{red} \to } \begin{bmatrix} 1 \\ 4 \\ \end{bmatrix} $$

直觉：只要 $A$ 没有 “坍缩”，$A$ 对应的变换就是可逆的

  • 逆变换只和 $A$ 有关，和等式右边无关
  • 求出 $A^{-1}$ 就能求解任意线性方程组！

高斯消元法

线性变换

  • 2D: 一个拉伸/旋转的平行四边形
  • 3D: 一个拉伸/旋转的平行六面体

如何把线性变换 “变回” 单位立方体？

  • 逐个坐标轴 “扳回” 单位向量
  • 贪心算法
    • 找到一个能使线性变换 “更正” 的线性变换 $X_i$
    • $X_k \cdot \ldots \cdot X_2 \cdot X_1 \cdot A = I$
      • $A^{-1} = X_k \cdot \ldots \cdot X_2 \cdot X_1 \cdot$

高斯消元中用到的两种线性变换

第三行所有系数乘以 $k$

  • $z$ 轴拉伸 $k$ 倍

$$ \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & k \\ \end{bmatrix} $$

第三行减去第一行

  • $z$ 轴向 $x$ 轴负方向旋转 45 度

$$ \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ -1 & 0 & 1 \\ \end{bmatrix} $$

高斯消元法

观察鸡兔同笼问题 “转过去” 再 “转回来” 的过程

$$ \begin{bmatrix} 1 & 1 \\ 2 & 4 \\ \end{bmatrix} \to \begin{bmatrix} 1 & 1 \\ 1 & 2 \\ \end{bmatrix} \to \begin{bmatrix} 1 & 1 \\ 0 & 1 \\ \end{bmatrix} \to \begin{bmatrix} 1 & 0 \\ 0 & 1 \\ \end{bmatrix} $$

  • JT3(JT2(JT1(JT(grid2d))))
  • 通用的算法
    • 目标：消除主对角线之外的所有元素
    • 方法：按照矩阵下三角的顺序消除

高斯消元法 (cont'd)

一些补充

  • 如果目标轴被别其他向量 “占据” 了： $$ \begin{bmatrix} 0 & 1 & 0 \\ 0 & 0 & 1 \\ 1 & 0 & 0 \\ \end{bmatrix} $$ 就需要 “换元” (排列也可以写成矩阵)
  • 如果 “目标轴” 和另一个向量很接近，就会引起计算误差

更一般的情形

刚才我们假设了 $A$ 是一个 3D → 3D 的映射

  • 如果 $A$ 是 “坍缩” 的呢？
    • 有更多的 $x$ 使得 $Ax = 0$！
    • 再次观察坍缩的过程

$Ax = 0$ 和 $Ax \ne 0$ 包含了空间中的所有点

  • 它们是 “垂直” 的！

总结

线性变换视角的矩阵

最符合人类直觉感受的理解方法

$$ \begin{bmatrix} 1 \\ 0 \\ 0 \end{bmatrix} { \color{red} \to } \begin{bmatrix} a \\ b \\ c \end{bmatrix} \qquad \begin{bmatrix} 0 \\ 1 \\ 0 \end{bmatrix} { \color{red} \to } \begin{bmatrix} d \\ e \\ f \end{bmatrix} \qquad \begin{bmatrix} 0 \\ 0 \\ 1 \end{bmatrix} { \color{red} \to } \begin{bmatrix} g \\ h \\ i \end{bmatrix} $$

End.


3Blue1Brown: 线性代数的本质